martedì, novembre 21, 2006
Cellular Neural Networks (CNN)
Gli automi cellulari sono sempre stati considerati dei giochini interessanti, fatti per esplorare le basi più semplici della teoria del caos, osservare comportamenti e proprietà emergenti non banalmente deducibili dalle regole di evoluzione del sistema. La loro natura di "stati definiti su nodi du un lattige rettangolare bidimensionale" però li hanno sempre resi molto vicini alle problematiche di elaborazione delle immagini. Ecco qui un lavoro che permette di esplorare alcune tecniche di elaborazione di immagini basate sugli automi cellulari. Lo strumento teorico, estensione dell'automa cellulare classico, prende il nome di rete neurale cellulare (CNN). I risultati sono interessanti, anche se non mostrano nulla di non ottenibile per altre vie, in genere anche in maniera molto più efficiente.
L'idea di estendere però lo strumento affinchè sia in grado di gestire organizzazioni di cellulle in agglomerati capaci di computazione locale non sarebbe malaccio.. si immaginino delle sorte di agglomerati cellulari che si muovono nello spazio degli stati attingendo alle informazioni presenti in esso e nell'immagine, aggregazioni che magari tendono a nutrirsi di pixel a 1 nell'immagine (binaria) da elaborare, la loro evoluzione potrebbe portare ad agglomerati di cellule addensati dove sono presenti curve o aree, portando ad un perceptual grouping dei dati sparsi ed incompleti.
Potrebbe essere un campo divertente in cui giocare :)
L'idea di estendere però lo strumento affinchè sia in grado di gestire organizzazioni di cellulle in agglomerati capaci di computazione locale non sarebbe malaccio.. si immaginino delle sorte di agglomerati cellulari che si muovono nello spazio degli stati attingendo alle informazioni presenti in esso e nell'immagine, aggregazioni che magari tendono a nutrirsi di pixel a 1 nell'immagine (binaria) da elaborare, la loro evoluzione potrebbe portare ad agglomerati di cellule addensati dove sono presenti curve o aree, portando ad un perceptual grouping dei dati sparsi ed incompleti.
Potrebbe essere un campo divertente in cui giocare :)
Etichette:
elaborazione delle immagini,
teoria
lunedì, novembre 13, 2006
Flatlandia, quesito di Novembre 2006
Nel sito Flatlandia ogni mese viene proposto un quesito geometrico a cui provare a rispondere cimentandosi nella dimostrazione di piccoli teoremi oppure dove è possibile cimentarsi in divertenti costruzioni geometriche. Su questo blog verranno pubblicate le risposte.
Quesito di Novembre 2006:
La costruzione richiesta non è banale, ma può essere ottenuta ragionando sulla costruzione della bisettrice di un angolo dati tre punti (estremo, centro ed altro estremo), e sui gradi di libertà a disposizione. In particolare è possibile utilizzare un SW di geometria vincolata, come kseg, per costruire ciò che di seguito viene descirtto.
Quesito di Novembre 2006:
Costruire un quadrilatero in cui le bisettrici di due angoli opposti (di vertici A e C) siano parallele.
1) Quali caratteristiche presenta il quadrilatero così ottenuto?
2) Potrebbe essere un trapezio o un parallelogrammo?
Descrivere la costruzione e giustificare le risposte.
La costruzione richiesta non è banale, ma può essere ottenuta ragionando sulla costruzione della bisettrice di un angolo dati tre punti (estremo, centro ed altro estremo), e sui gradi di libertà a disposizione. In particolare è possibile utilizzare un SW di geometria vincolata, come kseg, per costruire ciò che di seguito viene descirtto.
- Il quadrilatero descritto ha 7 gradi di libertà: ovvero perde solamente un grado di libertà nel vincolo richiesto. E' quindi possibile pernsare di utilizzare 6 gradi di libertà per fissare 3 punti del quadrilatero, utilizzare il restante grado di libertà per selezionare la bisettrice parallela a quella (implicitamente) data e trovare quindi la costruzione che permetta di determinare il quarto punto.
- La costruzione di una bisettrice dati tre punti A, B e C è molto semplice, è sufficiente infatti:
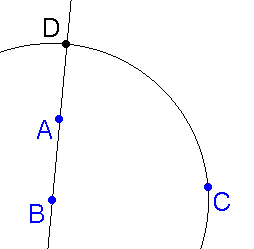
- Per ottenere ora il quarto punto del quadrilatero è indispensabile costruire una retta parallela alla bisettrice appena ottenuta controllabile tramite un punto; per questo motivo si costuisce un punto P libero sul segmento AC e si costruisce la retta passante per esso e parallela alla bisettrice.
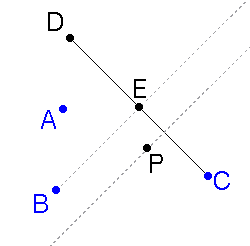
- Per costruzione, esattamente come per il segmento DC, il punto incognito X potrà essere utilizzato per costruire la bisettrice, a noi nota, utilizzando la stessa costruzione. Per questo motivo si costruisce il segmento passante per A e parallelo a DC, si determina il punto di incontro F con la bisettrice di X e si determina il punto proiettato D' a distanza doppiarispetto ad AF.
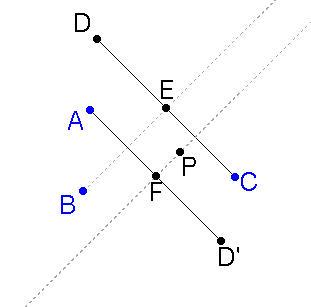
- A questo punto, esattamente come B è il punto di incontro tra le rette BE (bisettrice) ed AD, così è possibile costruire la retta CD' e determinare il quarto punto del quadrilatero come incrocio con la bisettrice nota.
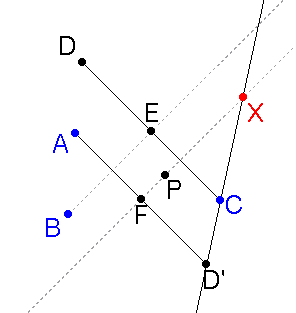
- L'output ottenuta con in input i punti A, B, C e P vincolato sul segmento AC è quello mostrato in figura.

- Interessante è osservare, al muoversi di P sul segmento AC, quali sono le possibili posizioni del punto X. Per ottenere questa informazione viene costruito il luogo di punti X definito dalle possibili posizioni di P ottenendo quanto mostrato nella figura seguente:

- Si può mostrare che le possibili posizioni del punto X si trovano su una roto-omotetia dell'iperbole equilatera limitata dai punti A e C e passante per B ed ovviamente X. Un ramo (quello superiore nella figura) consente di ottenere i quadrilateri convessi e l'altro consente di ottenere i quadrilateri concavi.
- Per quanto riguarda i quesiti: questa costruzione consente di avere tutti e soli i quadrilateri costruibili con le condizioni date, possono essere parallelogrammi ma non trapezi (se non degeneri in rettangoli).
mercoledì, novembre 08, 2006
Matlab: ottenere un numero arbitrario di parametri d'uscita
Spesso in Matlab capita di conoscere solo a run-time il numero di parametri da ottenere in uscita dalla chiamata a una funzione, questa situazione si presenta, ad esempio, se si utilizza la classica funzione ind2sub su un array di dimensionalità non nota a tempo di scrittura del codice.
Si immagini di avere a disposizione un array A ed un indice i di accesso lineare ai dati contenuti in A (accesso non strutturato, vedendo i semplicemente dati come una sequenza senza struttura). Ottenerne le dimensioni è possibile con la funzione size, ottenere l'indice strutturato da i richiede di ottenere in uscita dalla funzione ind2sub un numero di parametri non a tempo di scrittura del codice. L'utilizzo dell'espansione delle celle in sequenze di parametri viene in soccorso:
Si immagini di avere a disposizione un array A ed un indice i di accesso lineare ai dati contenuti in A (accesso non strutturato, vedendo i semplicemente dati come una sequenza senza struttura). Ottenerne le dimensioni è possibile con la funzione size, ottenere l'indice strutturato da i richiede di ottenere in uscita dalla funzione ind2sub un numero di parametri non a tempo di scrittura del codice. L'utilizzo dell'espansione delle celle in sequenze di parametri viene in soccorso:
% Ottenimento delle dimensioni:
sze = size(A);
% Costruzione della cella per i parametri in output:
is = cell(1,numel(sze));
% Conversione dell'indice i in indice strutturato:
[is{:}] = ind2sub(sze,i);
% Esempio di utilizzo degli indici strutturati memorizzati nella cella:
elem = A(is{:});
martedì, novembre 07, 2006
Lenta carne pensante
A volte, il peso del proprio corpo,
ci fa sentire legati
a una realtà terrena da cui fuggire;
lo si vorrebbe abbandonare,
seppur momentaneamente,
per inibirne le distrazioni,
per eliminare dalla mente
gli effetti dei suoi capricci.
M'immagino senza carne,
pensiero puro librante,
capace di incredibili voli pindarici
che mi portino ovunque:
nel cuore di persone fantastiche,
nel cuore di luoghi fantastici,
nel cuore di teorie fantastiche.
Ma il fardello è qui, da trasportare;
la realtà ci mantiene
in uno spazio-tempo limitato;
solo un sospiro e una carezza
possono dar l'illusione della libertà.
Chiudo gli occhi: per un attimo volo.
Tempo fuggevole, luoghi lontani,
li focalizzo chiaramente:
canyon, foreste, oceani e ghiacciai;
luoghi dove dispiegare le ali
d'una ricercata serenità.
Ne carezzo la freschezza,
ne vedo i bagliori,
ne respiro l'aria,
ne odo i silenzi.
Riapro gli occhi,
tornano i sensi,
strette pareti.
Mi opprimono,
mi soffocano.
Uccidono.
ci fa sentire legati
a una realtà terrena da cui fuggire;
lo si vorrebbe abbandonare,
seppur momentaneamente,
per inibirne le distrazioni,
per eliminare dalla mente
gli effetti dei suoi capricci.
M'immagino senza carne,
pensiero puro librante,
capace di incredibili voli pindarici
che mi portino ovunque:
nel cuore di persone fantastiche,
nel cuore di luoghi fantastici,
nel cuore di teorie fantastiche.
Ma il fardello è qui, da trasportare;
la realtà ci mantiene
in uno spazio-tempo limitato;
solo un sospiro e una carezza
possono dar l'illusione della libertà.
Chiudo gli occhi: per un attimo volo.
Tempo fuggevole, luoghi lontani,
li focalizzo chiaramente:
canyon, foreste, oceani e ghiacciai;
luoghi dove dispiegare le ali
d'una ricercata serenità.
Ne carezzo la freschezza,
ne vedo i bagliori,
ne respiro l'aria,
ne odo i silenzi.
Riapro gli occhi,
tornano i sensi,
strette pareti.
Mi opprimono,
mi soffocano.
Uccidono.
venerdì, novembre 03, 2006
Matlab: multidimensional array slicing
Si immagini di avere un array multidimensionale A con un numero di dimensioni non noto nel momento in cui si scrive il codice. Si immagini anche di avere a disposizione un array from contenente per ogni dimensione l'indice di partenza di un'operazione di slicing, e un arrai to contenente gli indici di arrivo. Ipotizzando di avere già svolto tutti i controlli sulle dimensioni e sugli indici si può effettuare lo slicing come segue:
- Si costruisce una cella contenente per ogni dimensione l'array di indici da utilizzare.
- Si utilizza l'espansione di celle in elenco di parametri accoppiato con l'operatore di slicing.
% Parametri forniti:
A = rand(3,3,3);
from = [1,2,1];
to = [3,2,2];
% Costruzione della cella (domanda: il ciclo è evitabile?):
D = numel(size(A));
inds = cell(1,D);
for i=1:D% Gli indici voluti:end
inds{i} = from(i):to(i);
% Lo slicing:
sliceA = A(inds{:});
Flatlandia, quesito di Ottobre 2006
Sul sito Flatlandia ogni mese viene proposto un quesito geometrico da risolvere con la sola logica e la sola geometria. Ecco la mia risposta al seguente quesito di Ottobre 2006:

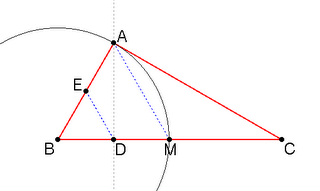
1) Fissato un segmento BC, costruire un triangolo ABC in cui la mediana AM sia congruente al lato AB.
2) Come si dovrà scegliere AM affinché il triangolo ABC sia rettangolo o acutangolo o ottusangolo?
Giustificare le risposte.

Nella figura è mostrata la costruzione che permette di ottenere il triangolo richiesto. In essa:
- Si è determinato il punto medio M sul segmento BC. Si è identificato il punto medio D sul segmento BM.
- Si è costruita la retta passante per D ortogonale a BM: questa retta è ortogonale alla corda della circonferenza passante per B ed M; preso un qualunque punto A su tale retta si ha che la distanza tra A e B è uguale alla distanza tra A ed M (mediana) essendo entrambe raggi della circonferenza costruita. Così è risolto il punto 1.

- Esistono solamente due punti A sulla retta passante per AD tali che il triangolo ottenuto sia rettangolo. Chiamati A1 ed A2 tali punti si ha che tutti i triangoli AiBC, in cui Ai è un punto sul segmento A1A2, sono ottusi. I triangoli A1BC e A2BC sono rettangoli e gli altri sono acuti.
- I punti A1 e A2 sono facilmente ottenibili grazie al seguente ragionamento: il triangolo finale, avendo un lato e due angoli in comune con ABD, deve essergli simile. Ma tracciandone la mediana DE come in figura, per similitudine deve essere DE congruente con BD, e quindi con DM, deve quindi essere la mediana la DE metà della mediana AM. Ne segue che il triangolo ABC è il doppio del triangolo ABD. Questo implica che, essendo AE, EB, ED, BD e DM congruenti, devono esserlo anche AB con BM, quindi il triangolo ABM è equilatero; è quindi sufficiente tracciare un arco centrato in B e passante per M per ottenere, come intersezione con la retta AD, i due punti A1 e A2. Così è risolto il punto 2.
Iscriviti a:
Post (Atom)

