1) Fissato un segmento BC, costruire un triangolo ABC in cui la mediana AM sia congruente al lato AB.
2) Come si dovrà scegliere AM affinché il triangolo ABC sia rettangolo o acutangolo o ottusangolo?
Giustificare le risposte.

Nella figura è mostrata la costruzione che permette di ottenere il triangolo richiesto. In essa:
- Si è determinato il punto medio M sul segmento BC. Si è identificato il punto medio D sul segmento BM.
- Si è costruita la retta passante per D ortogonale a BM: questa retta è ortogonale alla corda della circonferenza passante per B ed M; preso un qualunque punto A su tale retta si ha che la distanza tra A e B è uguale alla distanza tra A ed M (mediana) essendo entrambe raggi della circonferenza costruita. Così è risolto il punto 1.
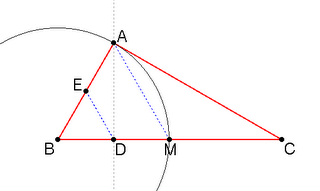
- Esistono solamente due punti A sulla retta passante per AD tali che il triangolo ottenuto sia rettangolo. Chiamati A1 ed A2 tali punti si ha che tutti i triangoli AiBC, in cui Ai è un punto sul segmento A1A2, sono ottusi. I triangoli A1BC e A2BC sono rettangoli e gli altri sono acuti.
- I punti A1 e A2 sono facilmente ottenibili grazie al seguente ragionamento: il triangolo finale, avendo un lato e due angoli in comune con ABD, deve essergli simile. Ma tracciandone la mediana DE come in figura, per similitudine deve essere DE congruente con BD, e quindi con DM, deve quindi essere la mediana la DE metà della mediana AM. Ne segue che il triangolo ABC è il doppio del triangolo ABD. Questo implica che, essendo AE, EB, ED, BD e DM congruenti, devono esserlo anche AB con BM, quindi il triangolo ABM è equilatero; è quindi sufficiente tracciare un arco centrato in B e passante per M per ottenere, come intersezione con la retta AD, i due punti A1 e A2. Così è risolto il punto 2.

Nessun commento:
Posta un commento