Quesito di Novembre 2006:
Costruire un quadrilatero in cui le bisettrici di due angoli opposti (di vertici A e C) siano parallele.
1) Quali caratteristiche presenta il quadrilatero così ottenuto?
2) Potrebbe essere un trapezio o un parallelogrammo?
Descrivere la costruzione e giustificare le risposte.
La costruzione richiesta non è banale, ma può essere ottenuta ragionando sulla costruzione della bisettrice di un angolo dati tre punti (estremo, centro ed altro estremo), e sui gradi di libertà a disposizione. In particolare è possibile utilizzare un SW di geometria vincolata, come kseg, per costruire ciò che di seguito viene descirtto.
- Il quadrilatero descritto ha 7 gradi di libertà: ovvero perde solamente un grado di libertà nel vincolo richiesto. E' quindi possibile pernsare di utilizzare 6 gradi di libertà per fissare 3 punti del quadrilatero, utilizzare il restante grado di libertà per selezionare la bisettrice parallela a quella (implicitamente) data e trovare quindi la costruzione che permetta di determinare il quarto punto.
- La costruzione di una bisettrice dati tre punti A, B e C è molto semplice, è sufficiente infatti:
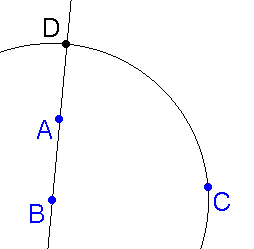
- Per ottenere ora il quarto punto del quadrilatero è indispensabile costruire una retta parallela alla bisettrice appena ottenuta controllabile tramite un punto; per questo motivo si costuisce un punto P libero sul segmento AC e si costruisce la retta passante per esso e parallela alla bisettrice.
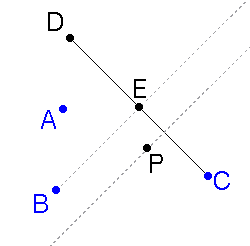
- Per costruzione, esattamente come per il segmento DC, il punto incognito X potrà essere utilizzato per costruire la bisettrice, a noi nota, utilizzando la stessa costruzione. Per questo motivo si costruisce il segmento passante per A e parallelo a DC, si determina il punto di incontro F con la bisettrice di X e si determina il punto proiettato D' a distanza doppiarispetto ad AF.
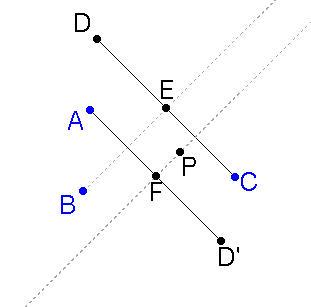
- A questo punto, esattamente come B è il punto di incontro tra le rette BE (bisettrice) ed AD, così è possibile costruire la retta CD' e determinare il quarto punto del quadrilatero come incrocio con la bisettrice nota.
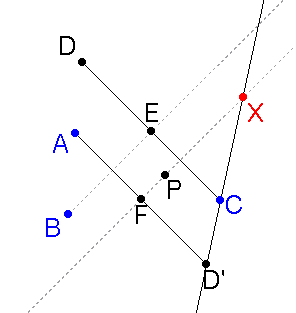
- L'output ottenuta con in input i punti A, B, C e P vincolato sul segmento AC è quello mostrato in figura.

- Interessante è osservare, al muoversi di P sul segmento AC, quali sono le possibili posizioni del punto X. Per ottenere questa informazione viene costruito il luogo di punti X definito dalle possibili posizioni di P ottenendo quanto mostrato nella figura seguente:

- Si può mostrare che le possibili posizioni del punto X si trovano su una roto-omotetia dell'iperbole equilatera limitata dai punti A e C e passante per B ed ovviamente X. Un ramo (quello superiore nella figura) consente di ottenere i quadrilateri convessi e l'altro consente di ottenere i quadrilateri concavi.
- Per quanto riguarda i quesiti: questa costruzione consente di avere tutti e soli i quadrilateri costruibili con le condizioni date, possono essere parallelogrammi ma non trapezi (se non degeneri in rettangoli).








1 commento:
Likato, ora!
Sim
Posta un commento